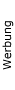Willkommen, Gast ( Anmelden | Registrierung )
  |
 20.07.2007, 01:36 20.07.2007, 01:36
Beitrag
#1
|
|||||||||
 Mitglied        Gruppe: Globaler Moderator Beiträge: 3577 Beigetreten: 15.09.2003 Wohnort: An der Ostseeküste Mitglieds-Nr.: 33 |
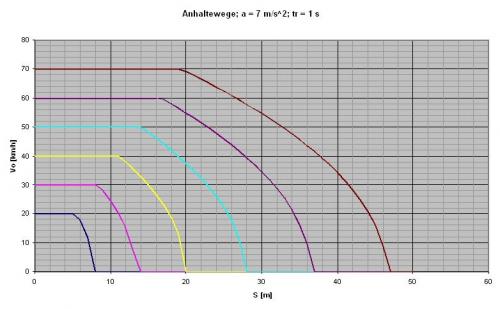
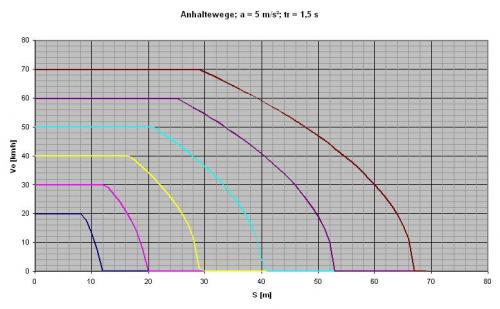
QUELLTEXT [URL=http://www.verkehrsportal.de/board/index.php?showtopic=55805]FAQ: Anhalteweg, Bremsweg , Reaktionsweg[/URL] Definition, Faustformeln und physikalische Herleitung Definitionen: Reaktionsweg ist die Strecke, die ein Fahrzeug in der Zeit zurücklegt, die der Fahrer braucht um eine Situation zu erkennen und mit dem Fuß anfängt das Bremspedal zu drücken. Die Geschwindigkeit ändert sich in dieser Zeit nicht. Bremsweg ist die Strecke, die ein Fahrzeug in der Zeit vom Drücken des Bremspedals bis zum Stillstand zurücklegt. Dabei verringert sich die Geschwindigkeit anfangs wenig und erst am Ende des Bremsweges stark (Grund siehe Herleitung). Anhalteweg ist die Strecke, die ein Fahrzeug vom Erkennen der Situation bis zum Stillstand zurücklegt, also die Summe aus Reaktions- und Bremsweg Faustformeln (kommen auch in der theoretischen Führerscheinprüfung vor): Reaktionsweg [Meter] = 3 x (Geschwindigkeit [km/h] / 10) Bremsweg [Meter] = (Geschwindigkeit [km/h] / 10) x (Geschwindigkeit [km/h] / 10) Gefahrbremsung = Bremsweg / 2 Anhalteweg = Reaktionsweg + Bremsweg Bei diesen Faustformeln wird eine Reaktionszeit von 1 Sekunde angenommen. Bei der normalen Bremsung wird eine Verzögerung von ca. 4m/sec² (man bemerkt eine deutliches Abbremsen, es ist aber noch nicht unangenehm) und bei der Gefahrbremsung von ca. 8m/sec² (die Reifen quitschen, es haut einen in die Gurte und ungesicherte Ladung fliegt nach vorne) angenommen. physikalisch Herleitung: (hier gilt ein besonder Dank @Hornblower, der hier einen hervorragenden Beitrag zum Thema geschrieben hat) Der Anhaltevorgang setzt sich zusammen aus der Reaktion und dem eigentlichen Bremsvorgang. Es gilt für den Anhalteweg: (0) 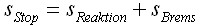 Der Reaktionsweg läßt sich recht einfach beschreiben: Man döst träge vor sich hin, und wie wir wissen, neigen träge Massen dazu, sich kräftefrei weiterzubewegen. Der Reaktionsweg läßt sich also trivial berechnen: (1) 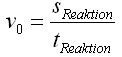 Mit: Vo: Anfangsgeschwindigkeit t(Reaktion): Reaktionszeit Stellen wir die Gleichung (01) um nach S(Reaktion), so erhalten wir: (2) 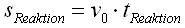 Für die Zeit t(Reaktion) gleiten wir also mit Vo dahin und legen die Strecke S(Reaktion) zurück. Nun endlich beginnen wir, zu bremsen. Gehen wir in erster Näherung von einer konstanten Verzögerung aus, so verändert sich unsere Geschwindigkeit als Funktion der Zeit gemäß: (3) 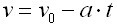 Mit: t: Zeit nach Einleiten der Bremsung V: Momentangeschwindigkeit zur Zeit t a: Bremsbeschleunigung Seit Beginn der Bremsung bis zum Zeitpunkt t legen wir einen Bremsweg S(Brems) zurück, der sich zusammensetzt denken lässt aus dem Teil der mit der konstanten Endgeschwindigkeit zurückgelegten Strecke und dem Teil der mit der linear abnehmenden Geschwindigkeit zurückgelegten Strecke: (4) 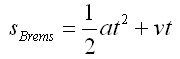 Erfolgt die Bremsung bis zum Stillstand, dann ist V = 0 und es bleibt nur noch der Streckenteil aus der linear abnehmenden Geschwindigkeit. Stellen wir Gleichung (3) nach t um, so erhalten wir: (5) 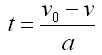 Einsetzen von (5) in Gleichung (4) führt uns zu: (6) 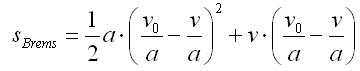 Anwendung der 2. Binomische Formel und Auflösen des hinteren Klammer-Terms liefert: (7) 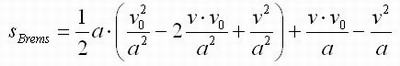 Auflösen des Klammer-Terms und Aufräumen bringt: (8)  Nach Erweitern des letzten Bruches um 2 und Zusammenfassen der Summanden kommen wir zu: (9) 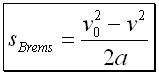 Diese Gleichung können wir nun einfach nach V auflösen und bekommen einen Zusammenhang, der uns die Geschwindigkeit als Funktion der Anfangsgeschwindigkeit, der Bremsverzögerung und der zurückgelegten Bremsstrecke beschreibt: (10) 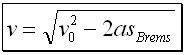 Im Folgenden wurden nun mit den Formeln (10) und (02) der Geschwindigkeits-Weg-Zusammenhang für den Anhalteprozes aus der Anfangsgeschwindigkeit Vo berechnet und graphisch dargestellt. Im ersten Fall wird von einer sehr guten Bremsverzögerung von a = 7 m/s² und einer schnellen Reaktion von 1 s ausgegangen. Im zweiten Fall wird von einer realistischeren Verzögerung von 5 m/s² ausgegangen (Otto-Normalauto, nichtoptimaler Straßenbelag und – wie mein Sicherheitstraining gezeigt hat – trauen sich viele Fahrer nicht, richtig in die Eisen zu gehen) sowie einer Reaktionszeit von 1,5 s (die für einen wirklich unvorbereiteten Fahrer eher zutrifft). Zusammenhang mit der „Faustformel für den Bremsweg": Bei der Bremsung bis zum Stillstand gilt für Momentangeschwindigkeit: Für den Bremsweg gilt: V = 0 Somit folgt: (11) 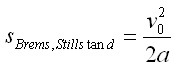 Die Faustformel für den Bremsweg ist: (12a) Bremsweg [Meter] = (Geschwindigkeit [km/h] / 10) x (Geschwindigkeit [km/h] / 10) Mit physikalisch korrekter Dimension bedeutet dies: (12b) 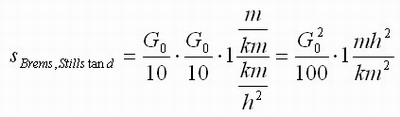 Gleichsetzen von (11) und (12b) führt zu: (13) 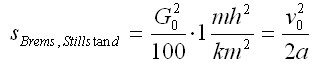 Für die Anfangsgeschwindigkeit in km/h gilt: (14) 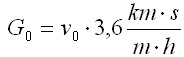 (14) in (13) führt zu: (15)  (16) 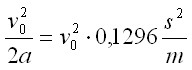 (17) 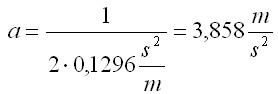 Die Fahrschul-Faustformel für den Bremsweg rechnet also mit einer Verzögerung von 3,858 m/s². Der Beitrag wurde von Tortenjan bearbeitet: 07.10.2008, 02:29
Bearbeitungsgrund: Abbildungen wieder richtig verlinkt
-------------------- errare humanum est
Zitat @mir "In jeder Gruppe gibt es immer so 5% Volltrottel" Zitat @Janus:"§0 StVO: "Man sieht doch, was gemeint ist!"" |
||||||||
|
|
|||||||||
|
|||||||||
 08.08.2007, 19:52 08.08.2007, 19:52
Beitrag
#2
|
|
 Mitglied         Gruppe: Globaler Moderator Beiträge: 13732 Beigetreten: 23.12.2004 Wohnort: HMS Lydia, Süd-Pazifik Mitglieds-Nr.: 7401 |
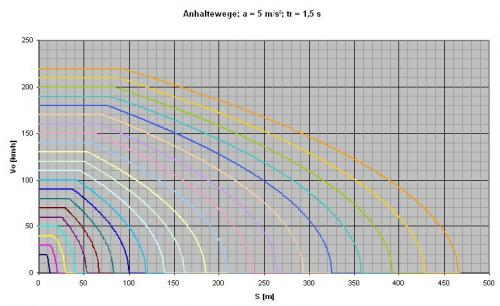
Diagramme zum Anhalteweg bei verschiedenen Bremsverzögerungen
Verzögerung: 3,86 m/s² (Faustformel) Reaktionszeit: 1 Sekunde 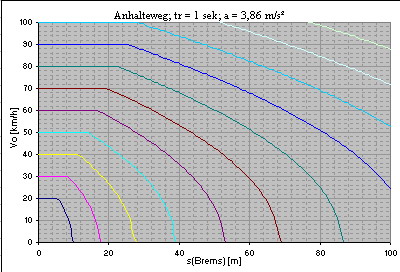  Verzögerung: 5 m/s² Reaktionszeit: 1 Sekunde  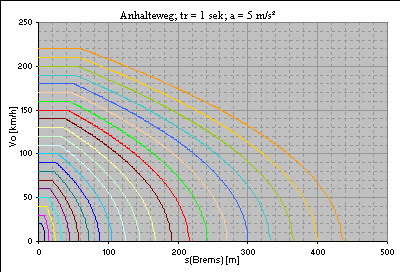 Verzögerung: 5 m/s² Reaktionszeit: 1,5 Sekunden 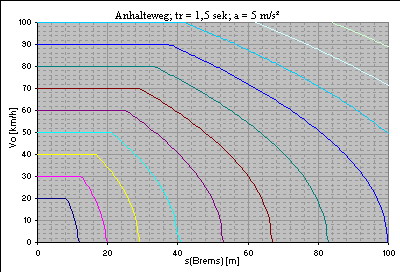 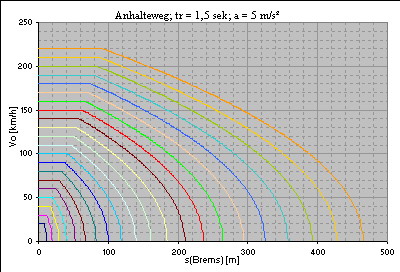 Verzögerung: 7,72 m/s² (Faustformel, Gefahrenbremsung) Reaktionszeit: 1 Sekunde 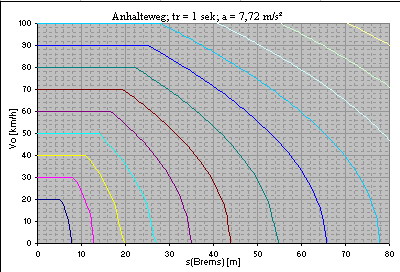 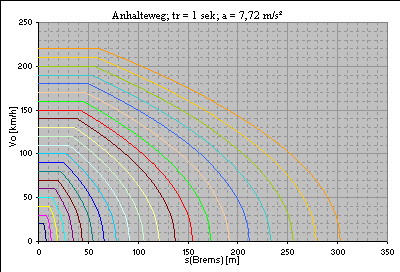 Verzögerung: 10 m/s² Reaktionszeit: 1 Sekunde 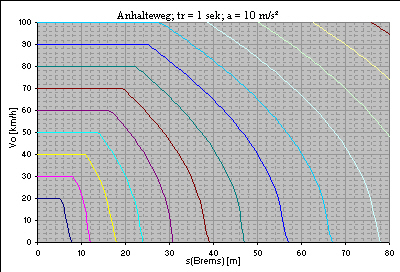 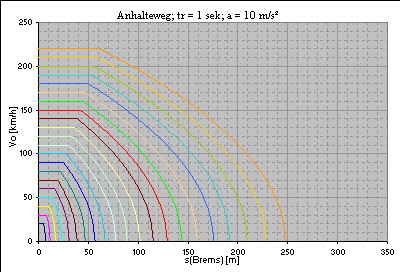
-------------------- Interessante Links: Alkohol-Abstinenznachweise Cut-Offs Haar-Analyse Cannabis VP-Abbau-Statistik Maastricht-Diagramme Amphetamine Kokain MPU-Beratung
----------- "Gendern" - dat is, wenn dem Sachsen sein Boot umkippt. |
|
|
|
  |
1 Besucher lesen dieses Thema (Gäste: 1 | Anonyme Besucher: 0)
0 Mitglieder:

|
Vereinfachte Darstellung | Aktuelles Datum: 23.11.2024 - 22:42 |